빅데이터 탐색
1 데이터 정제
데이터 정제
1. 데이터 종류
- 단변량 데이터: 데이터 특성이 하나인 데이터 ex) 재료비로 오리 가격 예측하겠다
- 다변량 데이터: 데이터 특성이 2개 이상인 데이터 ex) 재료비, 인건비로 오리 가격 예측하겠다.
- 시계열 데이터: 시간 순에 따라 관측된 데이터
2. 데이터 정제
- 집계: 데이터 요약(합계, 평균, 분산, 개수, min/max)
- 일반화: 데이터 일반 특성 추출
- 정규화: 데이터 정해진 구간 조정하여 상대적 차이 제거
- 평활화: 잡음 제거해 추세를 부드럽게 함. 시계열 데이터 분석에서 주로 사용 (이동/지수 평균법)
데이터 결측값 처리
1. 결측값 처리
- 존재하지 않는 데이터. null/NA. 의미 있을 수 o
- 단순 대치법: 결측값 데이터 삭제
- 평균 대치법: 평균으로 대치
- 회귀 대치법: 회귀분석 결과로 대치
- 단순 확률 대치법: 가까운 값으로 변경 (KNN 활용)
- 다중 대치법: 여러 번 대치 (대치 -> 분석 -> 결합)
데이터 이상값 처리
1. 이상값 처리
- 극단적으로 크거나 작은 값. 의미 있을 수 o
- 이상값 항상 제거는 XX
(1) ESD(Extreme Studentized Deviation)
- 평균으로부터 표준편차의 3배 넘는 데이터는 이상값으로 판단

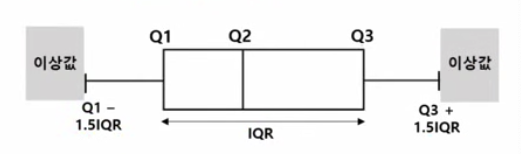
(2) 사분위수
- 1/4 보다 작거나 3/4보다 크면 이상값으로 판단
2. 분석 변수 처리
변수 선택
1. 변수 선택 방법
- 전진선택법: 변수를 하나씩 추가
- 후진제거법: 변수를 하나씩 제거
- 단계별 선택법: 전진선택법 + 후진선택법
- 상관관계 매트릭스 분석: 상관관계 가장 큰 거 2개 있으면 그 중 하나는 제거하자 느낌, 상관관계는 -1 ~ 1 사이의 값을 가지며, -1은 음의 상관관계, 1은 양의 상관관계를 의미
차원 축소
1. 차원의 저주
- 차원 높아질수록 알고리즘 성능이 저하
2. 주성분 분석(PCA)
- 차원 축소하여 새로운 변수 생성
- 분산이 가장 큰 축이 첫번째 주성분
- 70 ~ 90% 설명력 갖는 개수로 결정
3. 특이값 분해(SVD)
- MxN 크기 비정방행렬 A를 행렬 분해 (A = U시그마V^T)
파생변수 생성
1. 요약변수와 파생변수
- 요약변수: 수집 정보를 종합한 변수. 재활용성 높음 (1개월 수입)
- 파생변수: 의미 부여한 변수, 논리적 타당성 필요 (고객구매등급)
변수 반환
1. 수치형 자료와 범주형 자료
- 수치형 자료: 키, 몸무게
- 범주형 자료: 혈액형, 성별
2. 수치형 변수 변환
- Z-Score 정규화: 평균 0, 표준편차 1로 변환 ~ N(0,1)
**Z = x-평균/표준편차
- 최소-최대 정규화: 0~1 사이로 변환
X_new = x-min(x) / max(x)-min(x)
- 로그 변환: 로그를 취한 값으로 변환 (중간점이 좀 맞춰짐)
X_new = logX
3. 범주형 변수 변환
- 레이블 인코딩: 데이터를 정수로 변환 ex) A,B,C -> 0,1,2
- 원-핫 인코딩: 고유값 해당하는 컬럼만 1로 표시하고 나머지는 0으로. ex) A,B = [1,0],[0,1]
- 타깃 인코딩: 타깃변수를 평균값으로 반환
불균형 데이터 처리
1. 불균형 데이터 처리 방법
- 가중치 균형 적용: 불균형 데이터에 가중치
- 언더샘플링: 다수 데이터 일부만 선택 (랜덤/계통/집락/층화 추출법)
- 오버샘플링: 소수 데이터 복사 또는 유사하게 만듦 (SMOTE, ADSYN, ROS)
데이터 탐색
1. 데이터 탐색 기초
데이터 탐색 개요
1. EDA(탐색적 자료 분석)
- 데이터 의미 찾기 위해 통계, 시각화 통해 파악
- EDA 4가지 주제: 저항성 강조, 잔차 계산, 자료변수 재표현, 그래프 통한 현시성
> 저잔재현
상관관계 분석
1. 상관분석
- 두 변수 간 선형적 관계 파악하는 분석
- 피어슨 상관분석: 양적 척도, 연속형 변수, 선형관계 크기 측정
- 스피어만 상관분석: 서열 척도, 순서형 변수, 선형/비선형적 관계 나타냄
기초통계량 추출 및 이해
1. 기초 통계량
- 평균(기댓값): 전체 합을 개수로 나눈 값
- 중앙값: 자료 크기 순 나열 시 가운데 값
- 최빈값: 가장 빈번하게 등장하는 값
- 분산: 자료 퍼져있는 정보
- 표준편차: 분산 제곱근
- 공분산: 두 확률변수의 상관정도/ 0: 상관없음, >0: 양의 상관관계, <0: 음의 상관관계 / 최소최대값이 없어 강약 판단 불가
- 상관계수: 상관정도를 -1 ~ 1로 표현. / 1: 정비례관계, 0: 상관없음, -1: 반비례관계
2. 기댓값과 분산의 특성

3. 첨도와 왜도
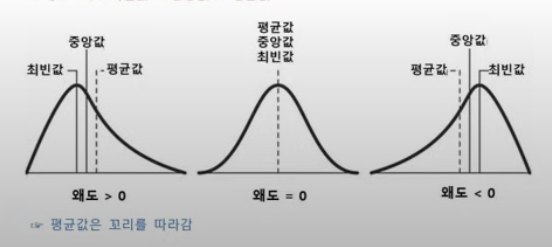
- 첨도: 자료의 분포가 얼마나 뾰족한지 나타내는 척도. 0 or 3: 정규 분포 형태. 값이 클수록 뾰족한 모양
- 왜도: 자료 분포의 비대칭 정도(0일 때 대칭)
- 왜도 < 0: 최빈값 > 중앙값 > 평균값
- 왜도 > 0: 최빈값 < 중앙값 < 평균값
4. Summary 함수 결과 해석

시각적 데이터 탐색
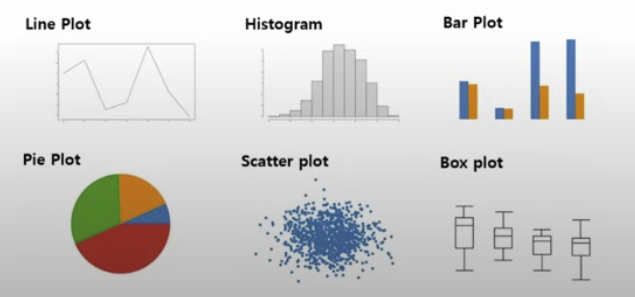
2. 고급 데이터 탐색
시공간 데이터 탐색
1. 시공간 데이터
- 공간적 정보 + 시간 흐름 결합된 데이터
- 활용: 시간적 패턴 통한 예측, 지도 통한 위치정보, 지리 격자 차트 결합
> 패지격
다변량 데이터 탐색
1. 다변량 데이터 탐색방법
- 주성분분석(PCA): 데이터 분포 분산이 최대가 되는 정보로 자원 축소
- 다차원척도법(MDS): 데이터 간 근접성을 시각화해 데이터 간 거리를 보존하여 차원 축소
- 로컬선형임베딩(LLE): 데이터 간 가까운 이웃에 선형적으로 연관되어 있는지 측정하여 저차원 좌표계 맵핑
비정형 데이터 탐색
1. 비정형 데이터 분석 방법
- 데이터 마이닝
- 방대한 데이터 속 규칙, 패턴 찾고 예측하는 분야
- 유형: 인공신경망, 의사결정트리, 회귀분석, 로지스틱회귀, 군집분석, 연관분석 등
- 텍스트 마이닝: 단어나 문장 속에서 유의미한 인사이트 찾아내는 분야
- 오피니언 마이닝: 단어나 문장 속에서 감정, 평판 등 도출 분야
통계기법 이해
1 기술 통계
표본표출
1. 전수 조사와 표본 조사
- 전수조사: 전체 조사. 시간, 비용 많이 소모
- 표본 조사: 일부 추출 모집단 분석
2. 표본 추출 방법
- 랜덤 추출법
- 계통 추출법: 번호 부여해 일정 간격으로 추출
- 집락 추출법: 여러 군집 나누고 군집 선택해 랜덤 추출, 군집 내 이질적 특징, 군집 간 동질적 특징
- 층화 추출법: 군집 내 동질적 특징, 군집 간 이질적 특징. 같은 비율로 추출 시, 비례 층화 추출법
- 복원, 비복원 추출: 복원 추출 - 추출됐던 데이터 다시 포함해 표본 추출 / 비복원 추출 - 추출됐던 데이터는 제외하고 표본 추출
확률 분포
1. 기초 확률 이론
- 조건부 확률: 특정 사건 B가 발생했을 때 A가 발생할 확률
- 독립 사건: A,B가 서로 영향 주지 않는 사건
- 배반 사건: A,B가 서로 동시에 일어나지 않는 사건
- 베이즈 정리: 두 확률 변수의 사전 확률과 사후 확률 사이의 관계를 나타내는 정리
2. 확률 분포
- 확률 변수가 특정 값을 가질 확률 을 나타내는 함수
(1) 이산 확률분포
- 값을 셀 수 있는 분포, 확률질량함수로 표현
- 이산균등분포: 모든 곳에서 값이 일정한 분포
- 베르노이분포: 매 시행마다 오직 2가지 결과뿐인 분포
- 이항분포: n번의 독립적인 베르누이 시행 통해 성공 확률 p를 가지는 분포
- 기하분포: 처음 성공 나올 때까지 시도 횟수를 확률 변수로 가지는 분포
- 다항분포: 여러 값 가질 수 있는 확률 변수들에 대한 분포
- 포아송분포: 단위 공간 내에서 발생할 수 있는 사건의 발생 횟수 표현하는 분포
> 베포항항하
(2) 연속 확률분포
- 값을 셀 수 없는 분포, 확률 밀도함수로 표현
- 정규분포: 일상생활에서 흔히 보는 가우스 분포(Z검정)
- t분포: 두 집단 평균치 차이의 비교 검정 시 사용 (T검정) / 데이터 개수가 30개 이상이면 정규성 검정 불필요
- 카이제곱분포: 두 집단의 동질성 검정 / 단일 집단 모분상에 대한 검정
- F분포: 두 집단의 분산의 동일성 검정 시 사용
(3) 확률변수 X의 f(x) 확률 분포에 대한 기대값(E(X))
- 이산적 확률 변수: E(x) = 시그마 xf(x)
- 연속적 확률변수: E(x) = 적분 xf(x)
표본분포
1. 표본집단의 표본분포
- 표본분포 평균 E(x) = 평균
- 표본분포의 분산 V(x) = 표준편차^2 / 표본 크기
2. 중심극한정리
- 표본 크기가 충분히 크면(30개) 정규분포
- 모집단 분포에 상관 없이 표본분포가 정규분포를 이룸
2. 추론통계
점추정
- 모집단이 특정 값으로 추정
구간추정
1. 구간추정
- 모집단이 특정 구간으로 추정 (95, 99%)
2. 모평균의 구간 추정

가설검정
1. 가설검정
- 모집단 특성에 대한 주장을 가설로 세우고, 표본 조사로 가설의 채택여부를 판정
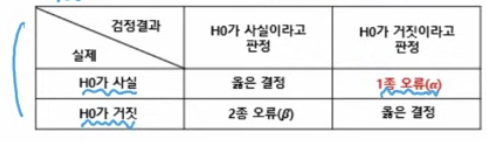
(1) 귀무가설(H0): 일반 가설
(2) 대립가설(H1): 귀무가설을 기각하는 가설, 증명하고자 하는 가설
(3) 유의수준(a) 귀무가설이 참일 때 기각하는 1종 오류를 범할 확률의 허용 한계 (보통 0.05)
(4) 기각역: 귀무가설이 기각되고 대립가설이 채택되는 검정통계량의 영역
2. 가설 검정 문제 풀이 방법
(1) 귀무가설/대립가설 설정
- 차이가 없다 혹은 동일하다 -> 귀무가설
(2) 양측 혹은 단측 검정 확인
- 같지 않으면 양측검증 해야하고, 값이 크거나 작으면 단측검정하면 됨
(3) 일표본(하나 표본), 이표본(2개 모집단)
(4) 검정통계량 계산과 기각역 판단
- 검정통계량이 기각역에 존재 -> 귀무가설 기각
- 검정통계량이 채택역에 존재 -> 귀무가설 채택
(5) t검정일 경우
- 모집단에 대한 평균검정이면 단일표본
- 동일 모집단에 대한 평균 비교면 대응표본
- 서로 다른 모집단에 대한 평균 비교면 독립표본

